One of the thermodynamic properties of a system is its internal energy, E, which is the sum of the kinetic and potential energies of the particles that form the system. The internal energy of a system can be understood by examining the simplest possible system: an ideal gas. Because the particles in an ideal gas do not interact, this system has no potential energy. The internal energy of an ideal gas is therefore the sum of the kinetic energies of the particles in the gas.
The kinetic molecular theory assumes that the temperature of a gas is directly proportional to the average kinetic energy of its particles, as shown in the figure below.
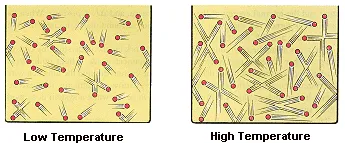
The internal energy of an ideal gas is therefore directly proportional to the temperature of the gas.
Esys = 3/2 RT
In this equation, R is the ideal gas constant in joules per mole kelvin (J/mol-K) and T is the temperature in kelvin.
The internal energy of systems that are more complex than an ideal gas can’t be measured directly. But the internal energy of the system is still proportional to its temperature. We can therefore monitor changes in the internal energy of a system by watching what happens to the temperature of the system. Whenever the temperature of the system increases we can conclude that the internal energy of the system has also increased.
Assume, for the moment, that a thermometer immersed in a beaker of water on a hot plate reads 73.5oC, as shown in the figure below. This measurement can only describe the state of the system at that moment in time. It can’t tell us whether the water was heated directly from room temperature to 73.5oC or heated from room temperature to 100oC and then allowed to cool.
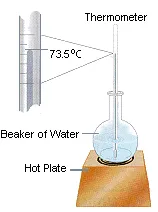
Temperature is therefore a state function. It depends only on the state of the system at any moment in time, not the path used to get the system to that state. Because the internal energy of the system is proportional to its temperature, internal energy is also a state function. Any change in the internal energy of the system is equal to the difference between its initial and final values.
Esys = Ef – Ei


Comments are closed.