To define a temperature scale that does not depend on the thermometric property of a substance, Carnot principle can be used since the Carnot engine efficiency does not depend on the working fluid. It depends on the temperatures of the reservoirs between which it operates.

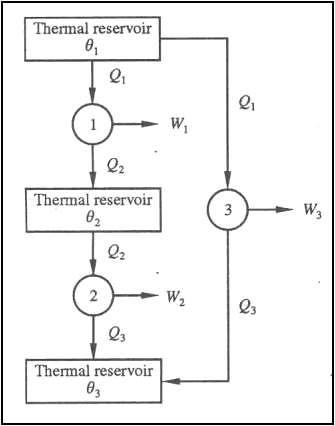
Consider the operation of three reversible engines 1, 2 and 3. The engine 1 absorbs energy Q₁ as heat from the reservoir at T₁, does work W₁ and rejects energy Q₂ as heat to the reservoir at T₂.

 Let the engine 2 absorb energy Q₂ as heat from the reservoir at T₂ and does work W₂ and rejects energy Q₃ as heat to the reservoir at T₃.

The third reversible engine 3, absorbs energy Q₁as heat from the reservoir at T₁, does work W₃ and rejects energy Q₃ as heat to the reservoir at T₃.

h₁ = W₁ / Q₁ = 1- Q₂/Q₁ = f(T₁,T₂)

or, Q₁/Q₂ = F(T₁,T₂)

h₂ = 1- Q₃/Q₂ = f(T₂,T₃)

or, T₂/T₃ = F(T₂,T₃)

h₃ = 1- Q₃/Q₁ = f(T₁,T₃)

T₁/T₃ = F(T₁,T₃)

Then , Q₁/Q₂ = (Q₁/Q₃)/(Q₂/Q₃)

Or, F(T₁,T₂) = F(T₁,T₃) /F(T₂,T₃)

Since T₃ does not appear on the left side, on the RHS also T₃ should cancel out. This is possible if the function F can be written as

F(T₁, T₂) = f(T₁) y (T₂)

f(T₁) y (T₂) = {f(T₁) y (T₃)} / {f(T₂) y (T₃)}

= f(T₁) y (T₂)

Therefore, y (T₂) = 1 / f(T₂)

Hence, Q₁ / Q₂ = F(T₁,T₂) = f(T₁)/ f(T₂)

Now, there are several functional relations that will satisfy this equation.

For the thermodynamic scale of temperature, Kelvin selected the relation

Q₁/Q₂ = T₁/T₂

That is, the ratio of energy absorbed to the energy rejected as heat by a reversible engine is equal to the ratio of the temperatures of the source and the sink.

The equation can be used to determine the temperature of any reservoir by operating a reversible engine between that reservoir and another easily reproducible reservoir and by measuring efficiency (heat interactions). The temperature of easily reproducible thermal reservoir can be arbitrarily assigned a numerical value (the reproducible reservoir can be at triple point of water and the temperature value assigned 273.16 K).